計算幾何は、Boost Geometry Libraryによって提供される。
インデックス
- 2つの図形が互いに素かを判定
- 2つの図形が交点を持っているかを判定
- 図形がもう一方の図形の完全な内側にあるかを判定
- 2つの図形が空間的に等しいかを判定
- 面積を計算する
- 図形の中心座標を計算する
- 図形の凸包を計算する
- 2つの図形の距離を計算する
- 2つの図形の差を計算する
- 2つの図形の和を計算する
- 2つの図形の共通部分を計算する
- 図形の包絡線を計算する
- 図形の長さを計算する
- 図形を逆向きにする
- 図形を単純化する
- 図形から重複した点を削除する
- 図形を平行移動する
- 図形を拡大縮小する
- 図形を回転する
2つの図形が互いに素かを判定
2つの図形が互いに素かを判定するには、boost::geometry::disjoint()アルゴリズムを使用する。
disjoint()関数は、2つの図形が重なりあっていなければtrue、重なり合っていたらfalseを返す。
box同士が重なりあっていないかを判定:
#include <boost/assert.hpp>
#include <boost/geometry/geometries/point_xy.hpp>
#include <boost/geometry/geometries/box.hpp>
#include <boost/geometry/algorithms/disjoint.hpp>
namespace bg = boost::geometry;
typedef bg::model::d2::point_xy<double> point;
typedef bg::model::box<point> box;
int main()
{
// A. disjoint
// a
// +------+
// | |
// | |
// +------+ b
// +------+
// | |
// | |
// +------+
{
const box a(point(0, 0), point(3, 3));
const box b(point(4, 4), point(7, 7));
const bool result = bg::disjoint(a, b);
BOOST_ASSERT(result);
}
// B. not disjoint
// a
// +------+
// | b |
// | +--+---+
// +---+--+ |
// | |
// +------+
{
const box a(point(0, 0), point(3, 3));
const box b(point(2, 2), point(5, 5));
const bool result = bg::disjoint(a, b);
BOOST_ASSERT(!result);
}
}
boxとpoint_xyが重なりあっていないかを判定:
#include <boost/assert.hpp>
#include <boost/geometry/geometries/point_xy.hpp>
#include <boost/geometry/geometries/box.hpp>
#include <boost/geometry/algorithms/disjoint.hpp>
namespace bg = boost::geometry;
typedef bg::model::d2::point_xy<double> point;
typedef bg::model::box<point> box;
int main()
{
// disjoint
// a
// +------+
// | |
// | |
// +------+
// b
{
const box a(point(0, 0), point(3, 3));
const point b(4, 4);
const bool result = bg::disjoint(a, b);
BOOST_ASSERT(result);
}
// not disjoint
// a
// +------+
// | b |
// | |
// +------+
{
const box a(point(0, 0), point(3, 3));
const point b(2, 2);
const bool result = bg::disjoint(a, b);
BOOST_ASSERT(!result);
}
}
2つの図形が交点を持っているかを判定
2つの図形が交点を持っているかを判定するには、boost::geometry::intersects()アルゴリズムを使用する。
2つの線が交わっているかの判定:
#include <boost/assert.hpp>
#include <boost/geometry.hpp>
#include <boost/geometry/geometries/linestring.hpp>
#include <boost/geometry/geometries/point_xy.hpp>
#include <boost/assign/list_of.hpp>
namespace bg = boost::geometry;
int main()
{
typedef bg::model::d2::point_xy<double> point;
// line2
// |
// ---+---- line1
// |
{
const bg::model::linestring<point> line1 = boost::assign::list_of<point>(0, 2)(2, 2);
const bg::model::linestring<point> line2 = boost::assign::list_of<point>(1, 0)(1, 4);
const bool result = bg::intersects(line1, line2);
BOOST_ASSERT(result); // 交点を持っている
}
// -------- line1
// -------- line2
{
const bg::model::linestring<point> line1 = boost::assign::list_of<point>(0, 0)(2, 0);
const bg::model::linestring<point> line2 = boost::assign::list_of<point>(0, 2)(2, 2);
const bool result = bg::intersects(line1, line2);
BOOST_ASSERT(!result); // 交点を持っていない
}
}
図形がもう一方の図形の完全な内側にあるかを判定
図形がもう一方の図形の内側にあるかを判定するには、boost::geometry::within()アルゴリズムを使用する。
within()関数は、第1引数の図形が、第2引数の図形の完全な内側にあればtrue、そうでなければfalseを返す。
点が四角形内にあるかを判定:
#include <iostream>
#include <boost/geometry/geometry.hpp>
namespace bg = boost::geometry;
typedef bg::model::d2::point_xy<double> point;
typedef bg::model::box<point> box;
int main()
{
const point top_left(0, 0);
const point bottom_right(3, 3);
const box box(top_left, bottom_right);
const point p(1.5, 1.5);
if (bg::within(p, box)) {
std::cout << "in" << std::endl;
}
else {
std::cout << "out" << std::endl;
}
}
出力結果:
in
2つの図形が空間的に等しいかを判定
2つの図形が空間的に等しいかを判定するには、boost::geometry::equals()アルゴリズムを使用する。
図形の形が同じでも位置が異なればfalseを返す。
以下は、三角形からなる四角形と、四角形が等しいか判定する処理:
#include <iostream>
#include <boost/geometry.hpp>
#include <boost/geometry/algorithms/equals.hpp>
#include <boost/geometry/geometries/polygon.hpp>
#include <boost/geometry/geometries/box.hpp>
#include <boost/geometry/geometries/adapted/boost_tuple.hpp>
#include <boost/assign/list_of.hpp>
BOOST_GEOMETRY_REGISTER_BOOST_TUPLE_CS(cs::cartesian)
namespace bg = boost::geometry;
// poly
// ae d
// +-----+
// | + |
// | + |
// +-----+
// b c
//
// box
// (0,0)
// +-----+
// | |
// | |
// +-----+
// (3,3)
int main()
{
typedef boost::tuple<int, int> point;
bg::model::polygon<point> poly;
bg::exterior_ring(poly) = boost::assign::tuple_list_of(0, 0)(0, 3)(3, 3)(3, 0)(0, 0);
const bg::model::box<point> box(point(0, 0), point(3, 3));
const bool result = bg::equals(poly, box);
if (result) {
std::cout << "equal" << std::endl;
}
else {
std::cout << "not equal" << std::endl;
}
}
実行結果:
equal
面積を計算する
図形の面積を計算するには、boost::geometry::area()関数を使用する。
以下は、四角形と三角形の面積を計算する例:
#include <iostream>
#include <boost/geometry.hpp>
#include <boost/geometry/geometries/point_xy.hpp>
#include <boost/geometry/geometries/box.hpp>
#include <boost/geometry/geometries/polygon.hpp>
#include <boost/assign/list_of.hpp>
namespace bg = boost::geometry;
int main()
{
typedef bg::model::d2::point_xy<double> point;
typedef bg::model::box<point> box;
typedef bg::model::polygon<point> polygon;
// box
{
const box x(point(0, 0), point(3, 3));
const double result = bg::area(x);
std::cout << result << std::endl;
}
// polygon
{
polygon x;
bg::exterior_ring(x) = boost::assign::list_of<point>(0, 0)(0, 3)(3, 3)(0, 0);
const double result = bg::area(x);
std::cout << result << std::endl;
}
}
実行結果:
9
4.5
図形の中心座標を計算する
図形の中心座標を計算するには、boost::geometry::centroid()か、boost::geometry::return_centroid<Point>()を使用する。
boost::geometry::centroid()関数は、中心座標の点を第2引数で参照として返し、boost::geometry::return_centroid()関数は、中心座標の点を戻り値で返す。
return_centroid()関数は、テンプレート引数でPoint Conceptの型を指定する必要がある。
三角形の中心座標を求める(centroidを使用):
#include <iostream>
#include <boost/geometry.hpp>
#include <boost/geometry/geometries/point_xy.hpp>
#include <boost/geometry/geometries/polygon.hpp>
#include <boost/assign/list_of.hpp>
namespace bg = boost::geometry;
int main()
{
typedef bg::model::d2::point_xy<double> point;
typedef bg::model::polygon<point> polygon;
polygon poly;
bg::exterior_ring(poly) = boost::assign::list_of<point>
(2, 0)
(4, 3)
(0, 3)
;
point p;
bg::centroid(poly, p);
std::cout << bg::dsv(p) << std::endl;
}
実行結果:
(1.55556, 1.66667)
return_centroidを使った場合:
#include <iostream>
#include <boost/geometry.hpp>
#include <boost/geometry/geometries/point_xy.hpp>
#include <boost/geometry/geometries/polygon.hpp>
#include <boost/assign/list_of.hpp>
namespace bg = boost::geometry;
int main()
{
typedef bg::model::d2::point_xy<double> point;
typedef bg::model::polygon<point> polygon;
polygon poly;
bg::exterior_ring(poly) = boost::assign::list_of<point>
(2, 0)
(4, 3)
(0, 3)
;
const point p = bg::return_centroid<point>(poly);
std::cout << bg::dsv(p) << std::endl;
}
実行結果:
(1.55556, 1.66667)
図形の凸包を計算する
図形の凸包を計算するには、boost::geometry::convex_hull()を使用する。
第1引数で図形を渡すと、第2引数で参照として凸包の図形が返される。
#include <iostream>
#include <boost/geometry.hpp>
#include <boost/geometry/geometries/polygon.hpp>
#include <boost/geometry/geometries/point_xy.hpp>
#include <boost/assign/list_of.hpp>
int main()
{
namespace bg = boost::geometry;
typedef bg::model::d2::point_xy<double> point;
typedef bg::model::polygon<point> polygon;
polygon poly;
bg::exterior_ring(poly) = boost::assign::list_of<point>
(2.0, 1.3)
(2.4, 1.7)
(3.6, 1.2)
(4.6, 1.6)
(4.1, 3.0)
(5.3, 2.8)
(5.4, 1.2)
(4.9, 0.8)
(3.6, 0.7)
(2.0, 1.3)
;
polygon hull;
bg::convex_hull(poly, hull);
std::cout
<< "polygon: " << bg::dsv(poly) << std::endl
<< "hull: " << bg::dsv(hull) << std::endl;
}
実行結果:
polygon: (((2, 1.3), (2.4, 1.7), (3.6, 1.2), (4.6, 1.6), (4.1, 3), (5.3, 2.8), (5.4, 1.2), (4.9, 0.8), (3.6, 0.7), (2, 1.3)))
hull: (((2, 1.3), (2.4, 1.7), (4.1, 3), (5.3, 2.8), (5.4, 1.2), (4.9, 0.8), (3.6, 0.7), (2, 1.3)))

緑色部分が入力した図形。点線部分が計算された凸包図形。
2つの図形の距離を計算する
2つの図形の距離を計算するには、boost::geometry::distance()関数を使用する。
distance()関数は、図形間の最短距離を返す。
点と点の距離:
#include <iostream>
#include <boost/geometry.hpp>
#include <boost/geometry/geometries/point_xy.hpp>
namespace bg = boost::geometry;
typedef bg::model::d2::point_xy<double> point;
int main()
{
const point a(0, 0);
const point b(3, 3);
const double d = bg::distance(a, b);
std::cout << d << std::endl;
}
実行結果:
4.24264
点と三角形の距離:
#include <iostream>
#include <boost/geometry.hpp>
#include <boost/geometry/geometries/point_xy.hpp>
#include <boost/geometry/geometries/polygon.hpp>
#include <boost/assign/list_of.hpp>
namespace bg = boost::geometry;
typedef bg::model::d2::point_xy<double> point;
typedef bg::model::polygon<point> polygon;
int main()
{
const point p(0, 0);
polygon poly;
bg::exterior_ring(poly) = boost::assign::list_of<point>
(3, 3)
(6, 3)
(6, 6)
(3, 3)
;
const double d = bg::distance(p, poly);
std::cout << d << std::endl;
}
実行結果:
4.24264
2つの図形の差を計算する
2つの図形の差を計算するには、boost::geometry::difference()関数を使用する。
第1引数と第2引数で渡した図形の差が、第3引数で返される。
#include <iostream>
#include <vector>
#include <boost/geometry.hpp>
#include <boost/geometry/geometries/point_xy.hpp>
#include <boost/geometry/geometries/polygon.hpp>
#include <boost/geometry/geometries/box.hpp>
#include <boost/assign/list_of.hpp>
namespace bg = boost::geometry;
typedef bg::model::d2::point_xy<double> point;
typedef bg::model::polygon<point> polygon;
typedef bg::model::box<point> box;
int main()
{
const box bx(point(2, 0), point(6, 4.5));
polygon poly;
bg::exterior_ring(poly) = boost::assign::list_of<point>
(1, 1)
(5, 5)
(5, 1)
(1, 1)
;
// bx - poly
std::vector<polygon> out;
bg::difference(bx, poly, out);
}
計算された差の図形:
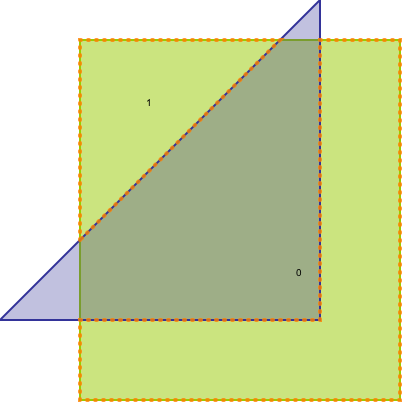
点線部分が、difference()関数で計算された図形。
2つの図形の和を計算する
2つの図形の和を計算するには、boost::geometry::union_()を使用する。
第1引数と第2引数で渡した図形の和が、第3引数で返される。
#include <iostream>
#include <vector>
#include <boost/geometry.hpp>
#include <boost/geometry/geometries/point_xy.hpp>
#include <boost/geometry/geometries/polygon.hpp>
#include <boost/geometry/geometries/box.hpp>
#include <boost/assign/list_of.hpp>
namespace bg = boost::geometry;
typedef bg::model::d2::point_xy<double> point;
typedef bg::model::polygon<point> polygon;
typedef bg::model::box<point> box;
int main()
{
const box bx(point(2, 0), point(6, 4.5));
polygon poly;
bg::exterior_ring(poly) = boost::assign::list_of<point>
(1, 1)
(5, 5)
(5, 1)
(1, 1)
;
std::vector<polygon> out;
bg::union_(bx, poly, out);
}
計算された和の図形:
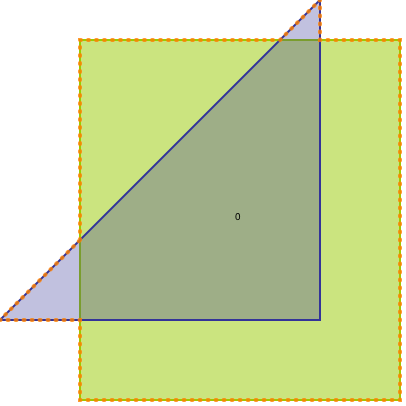
点線部分が、union_()関数で計算された図形。
注:union_()関数の名前がアンダーバーで終わっているのは、unionがC++言語仕様において予約語と定められているためである。
2つの図形の共通部分を計算する
2つの図形の共通部分を計算するには、boost::geometry::intersection()関数を使用する。
第1引数と第2引数で渡した図形の共通部分が、第3引数で返される。
#include <vector>
#include <boost/geometry.hpp>
#include <boost/geometry/geometries/point_xy.hpp>
#include <boost/geometry/geometries/polygon.hpp>
#include <boost/geometry/geometries/box.hpp>
#include <boost/assign/list_of.hpp>
namespace bg = boost::geometry;
typedef bg::model::d2::point_xy<double> point;
typedef bg::model::polygon<point> polygon;
typedef bg::model::box<point> box;
int main()
{
box bx(point(2, 0), point(6, 4.5));
polygon poly;
bg::exterior_ring(poly) = boost::assign::list_of<point>
(1, 1)
(5, 5)
(5, 1)
(1, 1)
;
std::vector<polygon> out;
bg::intersection(bx, poly, out);
}
計算された共通部分の図形:
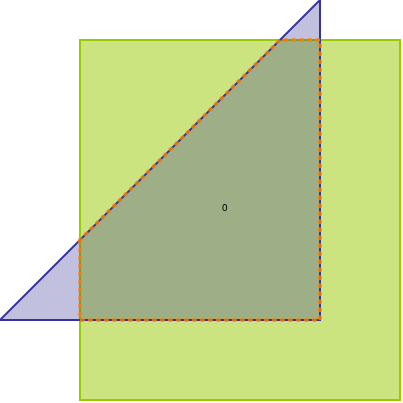
点線部分が、intersection()で計算された図形。
図形の包絡線を計算する
図形の包絡線を計算するには、boost::geometry::envelope()を計算する。
第1引数として渡した図形の包絡線が、Box Conceptの型として第2引数で返される。
#include <iostream>
#include <boost/geometry.hpp>
#include <boost/geometry/geometries/point_xy.hpp>
#include <boost/geometry/geometries/polygon.hpp>
#include <boost/geometry/geometries/box.hpp>
#include <boost/assign/list_of.hpp>
namespace bg = boost::geometry;
typedef bg::model::d2::point_xy<double> point;
typedef bg::model::polygon<point> polygon;
typedef bg::model::box<point> box;
int main()
{
polygon poly;
bg::exterior_ring(poly) = boost::assign::list_of<point>
(2.0, 1.3)
(2.4, 1.7)
(3.6, 1.2)
(4.6, 1.6)
(4.1, 3.0)
(5.3, 2.8)
(5.4, 1.2)
(4.9, 0.8)
(3.6, 0.7)
(2.0, 1.3)
;
box bx;
bg::envelope(poly, bx);
std::cout
<< "poly: " << bg::dsv(poly) << std::endl
<< "bx: " << bg::dsv(bx) << std::endl;
}
実行結果:
poly: (((2, 1.3), (2.4, 1.7), (3.6, 1.2), (4.6, 1.6), (4.1, 3), (5.3, 2.8), (5.4, 1.2), (4.9, 0.8), (3.6, 0.7), (2, 1.3)))
bx: ((2, 0.7), (5.4, 3))
計算された包絡線の図形:

点線部分が、envelope()で計算された包絡線。
また、boost::geometry::return_envelope<Box>()を使用すれば、参照ではなく戻り値として包絡線が返される。
#include <iostream>
#include <boost/geometry.hpp>
#include <boost/geometry/geometries/point_xy.hpp>
#include <boost/geometry/geometries/polygon.hpp>
#include <boost/geometry/geometries/box.hpp>
#include <boost/assign/list_of.hpp>
namespace bg = boost::geometry;
typedef bg::model::d2::point_xy<double> point;
typedef bg::model::polygon<point> polygon;
typedef bg::model::box<point> box;
int main()
{
polygon poly;
bg::exterior_ring(poly) = boost::assign::list_of<point>
(2.0, 1.3)
(2.4, 1.7)
(3.6, 1.2)
(4.6, 1.6)
(4.1, 3.0)
(5.3, 2.8)
(5.4, 1.2)
(4.9, 0.8)
(3.6, 0.7)
(2.0, 1.3)
;
const box bx = bg::return_envelope<box>(poly);
std::cout
<< "poly: " << bg::dsv(poly) << std::endl
<< "bx: " << bg::dsv(bx) << std::endl;
}
実行結果:
poly: (((2, 1.3), (2.4, 1.7), (3.6, 1.2), (4.6, 1.6), (4.1, 3), (5.3, 2.8), (5.4, 1.2), (4.9, 0.8), (3.6, 0.7), (2, 1.3)))
bx: ((2, 0.7), (5.4, 3))
図形の長さを計算する
図形の長さを計算するには、線の場合にはboost::geometry::length()関数を使用し、三角形の場合にはboost::geometry::perimeter()関数を使用する。
線の長さを計算
#include <iostream>
#include <boost/geometry.hpp>
#include <boost/geometry/geometries/point_xy.hpp>
#include <boost/geometry/geometries/linestring.hpp>
#include <boost/assign/list_of.hpp>
namespace bg = boost::geometry;
typedef bg::model::d2::point_xy<double> point;
int main()
{
bg::model::linestring<point> line = boost::assign::list_of<point>
(0, 0)
(1, 1)
(4, 8)
(3, 2)
;
const double len = bg::length(line);
std::cout << len << std::endl;
}
実行結果:
15.1127
三角形の長さを計算
#include <iostream>
#include <boost/geometry.hpp>
#include <boost/geometry/geometries/point_xy.hpp>
#include <boost/geometry/geometries/polygon.hpp>
#include <boost/assign/list_of.hpp>
namespace bg = boost::geometry;
typedef bg::model::d2::point_xy<double> point;
typedef bg::model::polygon<point> polygon;
int main()
{
polygon poly;
bg::exterior_ring(poly) = boost::assign::list_of<point>
(1, 1)
(5, 5)
(5, 1)
(1, 1)
;
const double len = bg::perimeter(poly);
std::cout << len << std::endl;
}
実行結果:
13.6569
図形を逆向きにする
図形を逆向きにするには、boost::geometry::reverse()を使用する。
#include <iostream>
#include <boost/geometry.hpp>
#include <boost/geometry/geometries/point_xy.hpp>
#include <boost/geometry/geometries/polygon.hpp>
#include <boost/assign/list_of.hpp>
namespace bg = boost::geometry;
typedef bg::model::d2::point_xy<double> point;
typedef bg::model::polygon<point> polygon;
int main()
{
polygon poly;
bg::exterior_ring(poly) = boost::assign::list_of<point>
(0, 0)
(3, 3)
(3, 1)
(0, 0)
;
bg::reverse(poly);
std::cout << bg::dsv(poly) << std::endl;
}
実行結果:
(((0, 0), (3, 1), (3, 3), (0, 0)))
図形を単純化する
図形を単純化するには、boost::geometry::simplify()を使用する。
- 第1引数 : 単純化する元となる図形
- 第2引数 : 出力先変数への参照
- 第3引数 : 単純化の距離
線を単純化する例:
#include <iostream>
#include <boost/geometry.hpp>
#include <boost/geometry/geometries/point_xy.hpp>
#include <boost/geometry/geometries/linestring.hpp>
#include <boost/assign/list_of.hpp>
namespace bg = boost::geometry;
typedef bg::model::d2::point_xy<double> point;
typedef bg::model::linestring<point> linestring;
int main()
{
const linestring line = boost::assign::list_of<point>
(3, 3)
(3.8, 4)
(6, 6)
(4, 9)
(5, 8)
(7, 7)
;
linestring result;
bg::simplify(line, result, 0.5);
std::cout << bg::dsv(line) << std::endl;
std::cout << bg::dsv(result) << std::endl;
}
実行結果:
((3, 3), (3.8, 4), (6, 6), (4, 9), (5, 8), (7, 7))
((3, 3), (6, 6), (4, 9), (7, 7))
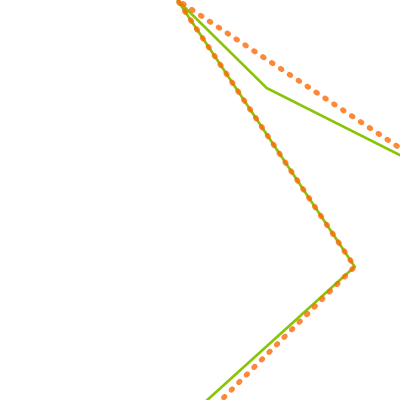
緑の実線が元となった図形。オレンジの点線がsimplify()によって単純化された図形。
図形から重複した点を削除する
重複した点を削除するには、boost::geometry::unique()関数を使用する。
#include <iostream>
#include <boost/geometry.hpp>
#include <boost/geometry/geometries/point_xy.hpp>
#include <boost/geometry/geometries/linestring.hpp>
#include <boost/assign/list_of.hpp>
namespace bg = boost::geometry;
typedef bg::model::d2::point_xy<double> point;
typedef bg::model::linestring<point> linestring;
int main()
{
linestring line = boost::assign::list_of<point>
(0, 0)
(1, 1)
(1, 1)
(3, 3)
(1, 1)
;
bg::unique(line);
std::cout << bg::dsv(line) << std::endl;
}
実行結果:
((0, 0), (1, 1), (3, 3), (1, 1))
図形を平行移動する
図形を平行移動するには、boost::geometry::transform()関数で、translate_transformer戦略ポリシーを使用して移動量を指定する。
#include <iostream>
#include <boost/geometry.hpp>
#include <boost/geometry/geometries/point_xy.hpp>
#include <boost/geometry/geometries/polygon.hpp>
#include <boost/assign/list_of.hpp>
namespace bg = boost::geometry;
namespace trans = bg::strategy::transform;
typedef bg::model::d2::point_xy<double> point;
typedef bg::model::polygon<point> polygon;
int main()
{
polygon poly;
bg::exterior_ring(poly) = boost::assign::list_of<point>
(0, 0)
(3, 3)
(3, 0)
(0, 0)
;
// (1.5, 1.5)移動する
// テンプレート引数:
// 1 : 点の要素を表す値型
// 2 : 変換元の次元数(最大3)
// 3 : 変換先の次元数(最大3)
// コンストラクタの引数
// 1 : xの移動量
// 2 : yの移動量
// 3 : zの移動量(省略可)
trans::translate_transformer<double, 2, 2> translate(1.5, 1.5);
polygon result;
bg::transform(poly, result, translate);
std::cout << bg::dsv(result) << std::endl;
}
実行結果:
(((1.5, 1.5), (4.5, 4.5), (4.5, 1.5), (1.5, 1.5)))
図形を拡大縮小する
図形を拡大縮小するには、boost::geometry::transform()関数に、scale_transformer戦略ポリシーを使用して拡大率を指定する。
#include <iostream>
#include <boost/geometry.hpp>
#include <boost/geometry/geometries/point_xy.hpp>
#include <boost/geometry/geometries/polygon.hpp>
#include <boost/assign/list_of.hpp>
namespace bg = boost::geometry;
namespace trans = bg::strategy::transform;
typedef bg::model::d2::point_xy<double> point;
typedef bg::model::polygon<point> polygon;
int main()
{
polygon poly;
bg::exterior_ring(poly) = boost::assign::list_of<point>
(0, 0)
(3, 3)
(3, 0)
(0, 0)
;
// 3倍に拡大する
// テンプレート引数:
// 1 : 点の要素を表す値型
// 2 : 変換元の次元数
// 3 : 変換先の次元数
// コンストラクタの引数
// 1 : 倍率
trans::scale_transformer<double, 2, 2> translate(3.0);
polygon result;
bg::transform(poly, result, translate);
std::cout << bg::dsv(result) << std::endl;
}
実行結果:
(((0, 0), (9, 9), (9, 0), (0, 0)))
図形を回転する
図形を回転するには、boost::geometry::transform()関数に、rotate_transformer戦略ポリシーを使用して回転する角度を指定する。
rotate_transformerのテンプレート引数で、角度の単位を選択できる。デグリ:boost::geometry::degree、ラジアン:boost::geometry::radian。
回転は、原点(0, 0)を中心に時計回りに行われる。
#include <iostream>
#include <boost/geometry.hpp>
#include <boost/geometry/geometries/point_xy.hpp>
#include <boost/geometry/geometries/polygon.hpp>
#include <boost/assign/list_of.hpp>
namespace bg = boost::geometry;
namespace trans = bg::strategy::transform;
typedef bg::model::d2::point_xy<double> point;
typedef bg::model::polygon<point> polygon;
int main()
{
polygon poly;
bg::exterior_ring(poly) = boost::assign::list_of<point>
(0, 0)
(3, 3)
(3, 0)
(0, 0)
;
trans::rotate_transformer<point, point, bg::degree> translate(90.0);
polygon result;
bg::transform(poly, result, translate);
std::cout << bg::dsv(result) << std::endl;
}
実行結果:
(((0, 0), (3, -3), (1.83691e-016, -3), (0, 0)))

緑の実線が回転前、オレンジの点線が回転後の図形。