グラフ構造とそれに対する操作を行うには、Boost Graph Libraryを使用する。
インデックス
- グラフ型を定義する
- 頂点と辺を追加する
- 任意のクラスをプロパティにする
- 頂点と辺のリストを取得する
- ダイクストラ法で最短経路を求める
- 最短経路の長さ(重みの合計)を求める
- ある頂点に到達可能かどうかを調べる
- 通過する辺が最も少ない経路を求める
- 2つのグラフが同型か判定する
- 最小全域木を作る
- トポロジカルソート
- 一筆書きの経路を求める
- グラフをGraphviz形式(.dot)で出力する
- Graphviz形式(.dot)のデータを読み込む
グラフ型を定義する
Boost.Graphで標準的に使用する、グラフ構造のためのクラスboost::adjacency_listは、様々な目的に利用できるようカスタマイズが可能になっている。
template <class OutEdgeListS = vecS,
class VertexListS = vecS,
class DirectedS = directedS,
class VertexProperties = no_property,
class EdgeProperties = no_property,
class GraphProperties = no_property,
class EdgeListS = listS>
class adjacency_list;
設定例:
以下は、無向グラフを定義する例:
typedef
boost::adjacency_list<
boost::listS,
boost::vecS,
boost::undirectedS
>
Graph;
有向グラフで、辺に重みを付ける例:
typedef
boost::adjacency_list<
boost::listS,
boost::vecS,
boost::directedS,
boost::no_property,
boost::property<boost::edge_weight_t, int>
>
Graph;
テンプレートパラメータの説明:
| パラメータ | 説明 | デフォルト |
|---|---|---|
OutEdgeList | グラフの隣接構造(入辺と出辺)を表すためのコンテナを指定する | vecS (std::vector) |
VertexList | グラフの頂点集合を表すためのコンテナを指定する | vecS (std::vector) |
DirectedS | 有向グラフか無向グラフかを選択する。directedS : 有向グラフundirectedS : 無向グラフbidirectionalS : 双方向グラフ(有向で、辺が2本) | directedS (有向グラフ) |
VertexProperties | 頂点のカスタムプロパティを指定する | no_property |
EdgeProperties | 辺のカスタムプロパティを指定する | no_property |
GraphProperties | グラフオブジェクトのカスタムプロパティを指定する | no_property |
EdgeListS | グラフの辺リストを表すためのコンテナを指定する。 このコンテナは、bidirectionalSもしくはundirectedSの場合に実際に辺を格納するために使用され、OutEdgeListはコンテナの要素を指すオブジェクトを格納する。directedSの場合はOutEdgeListに直接格納されるため、このパラメータは使用しない。 | listS (std::list) |
コンテナの選択
OutEdgeList, VertexList, EdgeListSパラメータでのコンテナの指定には、以下を指定できる:
| 指定可能なパラメータ | 説明 |
|---|---|
vecS | std::vector |
listS | std::list |
slistS | std::slist (非標準) |
setS | std::set |
multisetS | std::multiset |
hash_setS | boost::unordered_set |
hash_multisetS | boost::unordered_multiset |
プロパティの選択
VertexProperties, EdgeProperties, GraphPropertiesに指定可能な、標準提供されているプロパティは以下:
頂点プロパティ
| プロパティ | 説明 |
|---|---|
vertex_index_t | 順番 |
vertex_index1_t | 順番 |
vertex_index2_t | 順番 |
vertex_name_t | 名前 |
vertex_distance_t | 距離 |
vertex_root_t | ダイクストラや幅優先木での根を示す |
vertex_all_t | 頂点に関連づけられた全てのプロパティ |
vertex_color_t | 色 |
vertex_rank_t | ランク |
vertex_predecessor_t | 先行ノード |
vertex_isomorphism_t | 同型情報 |
vertex_invariant_t | 不変量(Wikipedia:不変量) |
vertex_invariant1_t | 不変量 |
vertex_invariant2_t | 不変量 |
vertex_degree_t | 次数(節点についてる辺の数) |
vertex_out_degree_t | 出次数(節点から出てる辺の数。無向の場合は次数と同じ) |
vertex_in_degree_t | 入次数(節点に入る辺の数。無効の場合は次数と同じ) |
vertex_discover_time_t | 深さ優先探索などでの発見された順番 |
vertex_finish_time_t | 深さ優先探索などでの探索が終わった順番 |
辺プロパティ
| プロパティ | 説明 |
|---|---|
edge_index_t | 順番 |
edge_name_t | 名前 |
edge_weight_t | 重み |
edge_weight2_t | 重み |
edge_capacity_t | キャパシティ |
edge_residual_capacity_t | 残りキャパシティ |
edge_reverse_t | 最大流アルゴリズムで使用する、向きが逆になった辺か否かを示す |
edge_all_t | 辺に関連づけられた全てのプロパティ |
グラフプロパティ
| プロパティ | 説明 |
|---|---|
graph_name_t | 名前 |
graph_all_t | グラフ自体に関連づけられた全てのプロパティ |
頂点と辺を追加する
頂点と辺を追加する方法としては、コンストラクタを使用するものと、boost::add_vertex()関数とboost::add_edge()関数を使用して動的に追加するものの2つがある。
1. コンストラクタを使用する
Boost.Graphのグラフ構造クラスは、コンストラクタで辺の範囲と頂点数をとる。
これを使用することで、シンプルにグラフを構築できる。
#include <utility>
#include <string>
#include <boost/graph/adjacency_list.hpp>
#include <boost/graph/graph_utility.hpp>
typedef boost::adjacency_list<boost::listS, boost::vecS, boost::directedS> Graph;
typedef std::pair<int, int> Edge;
enum { A, B, C, D, E, N };
const std::string name = "ABCDE";
int main()
{
const std::vector<Edge> edges = {
{A, B}, {A, C}, {A, D},
{B, E}, {C, E}, {D, E}
};
const Graph g(edges.begin(), edges.end(), N);
boost::print_graph(g, name.c_str());
}
出力:
A --> B C D
B --> E
C --> E
D --> E
E -->
2. 動的に追加する
コンストラクタは初期化時のみ使用可能なため、動的に頂点や辺を追加する必要がある場合には、頂点と追加するboost::add_vertex()関数、辺を追加するboost::add_edge()関数を使用する。
頂点を追加するboost::add_vertex()関数は、for文やwhile文でループして、必要な頂点数分だけ呼び出して使用する。戻り値として、頂点記述子が返される。
辺を追加するboost::add_edge()関数は、追加する辺の2つの頂点を指定して使用する。順番は、source、targetの順である。
#include <utility>
#include <string>
#include <boost/graph/adjacency_list.hpp>
#include <boost/graph/graph_utility.hpp>
typedef boost::adjacency_list<boost::listS, boost::vecS, boost::directedS> Graph;
typedef std::pair<int, int> Edge;
enum { A, B, C, D, E, N };
const std::string name = "ABCDE";
int main()
{
Graph g;
// 頂点を追加
std::map<int, Graph::vertex_descriptor> desc;
for (int i = 0; i < N; ++i) {
desc[i] = add_vertex(g);
}
// 辺を追加
add_edge(desc[A], desc[B], g);
add_edge(desc[A], desc[C], g);
add_edge(desc[A], desc[D], g);
add_edge(desc[B], desc[E], g);
add_edge(desc[C], desc[E], g);
add_edge(desc[D], desc[E], g);
boost::print_graph(g, name.c_str());
}
出力:
A --> B C D
B --> E
C --> E
D --> E
E -->
※add_vertex()関数とadd_edge()は、boost::adjacency_list以外のグラフ構造にも適用できるようにするため、名前空間の修飾なしで呼び出す。
参考:
任意のクラスをプロパティにする
Boost.Graphのグラフ構造には、Property Mapによって頂点・辺・グラフに任意のプロパティを持たせられる。しかしながらこの方法は、プロパティが増えてくると管理しきれなくなってくるので、ひとまとめにしたくなるだろう。
そこで、Boost.GraphにはBundleプロパティという機能が用意されている。これは、グラフ構造のプロパティ指定の場所にユーザー定義クラスを指定するという機能である。
後述のサンプルでは、以下のプロパティを設定している。
- 頂点のBundleプロパティとして「名前」「人口」「郵便番号一覧」を持つ
City(街)クラス - 辺のBundleプロパティとして「名前」と「距離」を持つ
Highway(高速道路)クラス - グラフのBundleプロパティとして「名前」を持つ
Country(国)クラス
そして、最短経路の計算の際に、Highwayクラスのdistanceメンバ変数を辺の重みとして使用している。
#include <iostream>
#include <string>
#include <boost/graph/adjacency_list.hpp>
#include <boost/graph/dijkstra_shortest_paths.hpp>
struct City {
std::string name;
int population;
std::vector<int> zipcodes;
};
struct Highway {
std::string name;
double distance; // km
};
struct Country {
std::string name;
};
typedef boost::adjacency_list<
boost::listS, boost::vecS, boost::bidirectionalS,
City, // 頂点のBundleプロパティ
Highway, // 辺のBundleプロパティ
Country // グラフのBundleプロパティ
> Map;
int main()
{
Map map;
// グラフのBundleプロパティを設定
map[boost::graph_bundle].name = "Japan";
// 街(頂点)を2つ追加
Map::vertex_descriptor v1 = add_vertex(map);
Map::vertex_descriptor v2 = add_vertex(map);
// 頂点のBundleプロパティを設定
map[v1].name = "Tokyo";
map[v1].population = 13221169;
map[v1].zipcodes.push_back(1500013);
map[v2].name = "Nagoya";
map[v2].population = 2267048;
map[v2].zipcodes.push_back(4600006);
// 辺を追加
bool inserted = false;
Map::edge_descriptor e;
boost::tie(e, inserted) = add_edge(v1, v2, map);
// 辺のBundleプロパティを設定
map[e].name = "Tomei Expessway";
map[e].distance = 325.5;
// Highwayクラスのdistanceメンバを辺の重みとして計算
std::vector<double> distance(boost::num_vertices(map));
boost::dijkstra_shortest_paths(map, v1,
boost::weight_map(boost::get(&Highway::distance, map)).
distance_map(&distance[0]));
std::cout << "Tokyo-Nagoya : " << distance[v2] << "km" << std::endl;
}
出力
Tokyo-Nagoya : 325.5km
頂点と辺のリストを取得する
グラフオブジェクトから頂点と辺のリストを取得するには、それぞれvertices()非メンバ関数とedges()非メンバ関数を使用する。
これらの関数は、頂点記述子もしくは辺記述子を要素とするリストの、イテレータの組を返す。
これらの機能を使用して、バンドルプロパティの例で作成したグラフの情報を列挙してみよう。
#include <iostream>
#include <string>
#include <boost/graph/adjacency_list.hpp>
struct City {
std::string name;
int population;
std::vector<int> zipcodes;
};
struct Highway {
std::string name;
double distance; // km
};
typedef boost::adjacency_list<
boost::listS, boost::vecS, boost::bidirectionalS,
City, // 頂点のBundleプロパティ
Highway // 辺のBundleプロパティ
> Map;
int main()
{
Map map;
// 街(頂点)を2つ追加
Map::vertex_descriptor v1 = add_vertex(map);
Map::vertex_descriptor v2 = add_vertex(map);
// 頂点のBundleプロパティを設定
map[v1].name = "Tokyo";
map[v1].population = 13221169;
map[v1].zipcodes.push_back(1500013);
map[v2].name = "Nagoya";
map[v2].population = 2267048;
map[v2].zipcodes.push_back(4600006);
// 辺を追加
bool inserted = false;
Map::edge_descriptor e;
boost::tie(e, inserted) = add_edge(v1, v2, map);
// 辺のBundleプロパティを設定
map[e].name = "Tomei Expessway";
map[e].distance = 325.5;
// 頂点を列挙
// vertices()関数は、グラフオブジェクトを引数にとり、
// 頂点リストのイテレータ範囲としてstd::pair<Iterator, Iterator>型を返す。
std::cout << "vertices :" << std::endl;
auto vertex_range = vertices(map);
for (auto first = vertex_range.first, last = vertex_range.second; first != last; ++first) {
Map::vertex_descriptor v = *first;
std::cout << " " << map[v].name << std::endl;
}
// 辺を列挙
// edges()関数は、グラフオブジェクトを引数にとり、
// 辺リストのイテレータ範囲としてstd::pair<Iterator, Iterator>型を返す。
std::cout << "edges :" << std::endl;
auto edge_range = edges(map);
for (auto first = edge_range.first, last = edge_range.second; first != last; ++first) {
Map::edge_descriptor e = *first;
std::cout << " " << map[e].name << std::endl;
}
}
出力
vertices :
Tokyo
Nagoya
edges :
Tomei Expessway
vertices()とedges()はイテレータの組を返すため、扱いが少々むずかしい。これを簡単にイテレーションさせるためには、以下のような方法がある:
BOOST_FOREACHマクロを使用する- イテレータの組を範囲for文で使用できる形式に変換する
BOOST_FOREACHマクロは、イテレータの組を範囲と見なすようになっているため、vertices()とedges()の戻り値を直接扱える:
#include <boost/foreach.hpp>
…
BOOST_FOREACH (Map::vertex_descriptor v : vertices(map)) {
}
C++11の範囲for文は、begin()/end()メンバ関数を持っていること、もしくは非メンバ関数のbegin(x)/end(x)でxオブジェクトに対するイテレータを取得できることが要求される。イテレータの組を、そのどちらかの形式に変換することで、範囲for文でvertices()/edges()を扱えるようになる。
身近なところでは、Boost.Rangeライブラリのboost::make_iterator_range()関数にイテレータの組を渡すことで、begin()/end()メンバ関数を持つ型に変換できる:
#include <boost/range/iterator_range_core.hpp>
for (Map::vertex_descriptor v : boost::make_iterator_range(vertices(map))) {
}
ほかにも、std名前空間に、std::pair<Iterator, Iterator>に対するstd::begin()/std::end()非メンバ関数のオーバーロードを追加する方法もあるが、std名前空間に機能を追加することは規約違反であるため、説明やかんたんなお試しコード以外の用途では推奨しない。
ダイクストラ法で最短経路を求める
ダイクストラ法で最短経路を求めるには、boost::dijkstra_shortest_paths()関数を使用する。
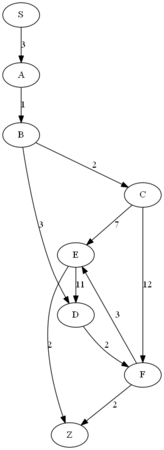
ここでは、以下の経路図で、頂点Sから頂点Zへの最短経路を求める。
経路図:
#include <iostream>
#include <vector>
#include <deque>
#include <string>
#include <boost/graph/adjacency_list.hpp>
#include <boost/graph/dijkstra_shortest_paths.hpp>
#include <boost/assign/list_of.hpp>
typedef boost::adjacency_list<boost::listS, boost::vecS, boost::directedS,
boost::no_property, boost::property<boost::edge_weight_t, int> > Graph;
typedef std::pair<int, int> Edge;
typedef boost::graph_traits<Graph>::vertex_descriptor Vertex;
enum { S, A, B, C, D, E, F, Z, N };
const std::string Names = "SABCDEFZ";
// グラフを作る
Graph make_graph()
{
const std::vector<Edge> edges = boost::assign::list_of<Edge>
(S, A)
(A, B)
(B, C)
(B, D)
(C, E)
(C, F)
(D, F)
(E, D)
(F, E)
(E, Z)
(F, Z)
;
const std::vector<int> weights = boost::assign::list_of
(3)
(1)
(2)
(3)
(7)
(12)
(2)
(11)
(3)
(2)
(2)
;
return Graph(edges.begin(), edges.end(), weights.begin(), N);
}
int main()
{
const Graph g = make_graph();
const Vertex from = S; // 開始地点
const Vertex to = Z; // 目的地
// 最短経路を計算
std::vector<Vertex> parents(boost::num_vertices(g));
boost::dijkstra_shortest_paths(g, from,
boost::predecessor_map(&parents[0]));
// 経路なし
if (parents[to] == to) {
std::cout << "no path" << std::endl;
return 1;
}
// 最短経路の頂点リストを作成
std::deque<Vertex> route;
for (Vertex v = to; v != from; v = parents[v]) {
route.push_front(v);
}
route.push_front(from);
// 最短経路を出力
for (const Vertex v : route) {
std::cout << Names[v] << std::endl;
}
}
出力
S
A
B
D
F
Z
この場合、SからZへの最短経路は、S, A, B, D, F, Zの順となる。
dijkstra_shortest_paths()関数の第1引数はグラフ構造を表す変数へのconst参照、第2引数は開始地点の頂点、第3引数は先行ノードを格納する変数へのポインタである。
目的地から開始地点まで先行ノードを辿っていくことにより、最短経路を求めることができる。
最短経路の長さ(重みの合計)を求める
最短経路の長さを求めるにはDistanceMapを使用する。DistanceMapは、最短経路探索の結果として取得できる、開始地点から最短経路のある頂点までの距離を保存したものである。
DistanceMapは、最短経路探索アルゴリズムにboost::distance_map()関数を使用して取得できる(他の名前付き引数に続けて記述する場合は、「named_param.distance_map(...);」のようにする)。
ここでは、先行ノードも一緒に求めているが、経路長のみが必要であれば、DistanceMapのみを計算してもよい。
#include <iostream>
#include <vector>
#include <deque>
#include <string>
#include <boost/graph/adjacency_list.hpp>
#include <boost/graph/dijkstra_shortest_paths.hpp>
#include <boost/assign/list_of.hpp>
typedef boost::adjacency_list<boost::listS, boost::vecS, boost::directedS,
boost::no_property, boost::property<boost::edge_weight_t, int> > Graph;
typedef std::pair<int, int> Edge;
typedef boost::graph_traits<Graph>::vertex_descriptor Vertex;
enum { S, A, B, C, D, E, F, Z, N };
const std::string Names = "SABCDEFZ";
// グラフを作る
Graph make_graph()
{
const std::vector<Edge> edges = boost::assign::list_of<Edge>
(S, A)
(A, B)
(B, C)
(B, D)
(C, E)
(C, F)
(D, F)
(E, D)
(F, E)
(E, Z)
(F, Z)
;
const std::vector<int> weights = boost::assign::list_of
(3)
(1)
(2)
(3)
(7)
(12)
(2)
(11)
(3)
(2)
(2)
;
return Graph(edges.begin(), edges.end(), weights.begin(), N);
}
int main()
{
const Graph g = make_graph();
const Vertex from = S; // 開始地点
const Vertex to = Z; // 目的地
std::vector<Vertex> parents(boost::num_vertices(g));
std::vector<std::size_t> distance(boost::num_vertices(g));
// 最短経路を計算
boost::dijkstra_shortest_paths(g, from,
boost::predecessor_map(&parents[0]).distance_map(&distance[0]));
// 経路なし
if (parents[to] == to) {
std::cout << "no path" << std::endl;
return 1;
}
// 最短経路の頂点リストを作成
std::deque<Vertex> route;
for (Vertex v = to; v != from; v = parents[v]) {
route.push_front(v);
}
route.push_front(from);
// 経路の長さを計算
const std::size_t n = distance[to];
std::cout << "route length:" << n << std::endl;
// 最短経路を出力
for (const Vertex v : route) {
std::cout << Names[v] << std::endl;
}
}
出力:
route length:11
S
A
B
D
F
Z
ある頂点に到達可能かどうかを調べる
ある頂点に到達可能かどうかを調べるには、<boost/graph/graph_utility.hpp>で定義されるboost::is_reachable()関数を使用する。この関数は、グラフ構造gにおいて、頂点xが頂点yに到達可能かどうかを調べ、到達可能であればtrue、そうでなければfalseを返す。
boost::is_reachable()の定義:
// <boost/graph/graph_utility.hpp>
namespace boost {
// xからyに到達可能?
template <typename IncidenceGraph, typename VertexColorMap>
bool is_reachable(
typename graph_traits<IncidenceGraph>::vertex_descriptor x,
typename graph_traits<IncidenceGraph>::vertex_descriptor y,
const IncidenceGraph& g,
VertexColorMap color // 各頂点が白で開始しなければならない
);
}
#include <iostream>
#include <cassert>
#include <vector>
#include <boost/graph/adjacency_list.hpp>
#include <boost/graph/graph_utility.hpp>
#include <boost/assign/list_of.hpp>
#include <boost/detail/lightweight_test.hpp>
typedef boost::adjacency_list<boost::listS, boost::vecS, boost::undirectedS> Graph;
typedef std::pair<int, int> Edge;
enum { A, B, C, D, E, N };
const int vertex_count = N;
int main()
{
const std::vector<Edge> edges = boost::assign::list_of<Edge>
(A, B)(B, E)
(A, C)(C, E)
; // Dはどこにも繋がっていない
const Graph g(edges.begin(), edges.end(), vertex_count);
// 全部白のカラーマップを作って渡す
std::vector<boost::default_color_type> color(vertex_count, boost::white_color);
// AからEに到達可能か調べる
if (boost::is_reachable(A, E, g, color.data())) {
std::cout << "AからEに到達可能" << std::endl;
}
else {
assert(false);
}
// AからDに到達可能か調べる
if (!boost::is_reachable(A, D, g, color.data())) {
std::cout << "AからDに到達不可能" << std::endl;
}
else {
assert(false);
}
}
出力:
AからEに到達可能
AからDに到達不可能
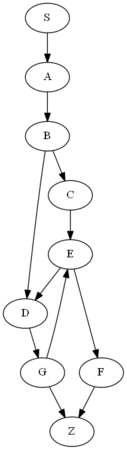
通過する辺が最も少ない経路を求める
辺に重みのないグラフから最短経路を求めると、「最短単純路」という通過する辺が最も少ない経路が得られる。これは、たとえばソーシャルグラフから「Twitterで何回のRTで特定の情報に辿りつけたか」というような情報を抽出する用途に使える。
~~Boost.Graphのboost::dijkstra_shortest_paths()は重みのないグラフを与えるとコンパイルエラーになるので、辺の重みを全て1に設定することで代用できる。~~
※2014/02/16 修正:そのような場面では Breadth-First Search を使うべきである。
#include <iostream>
#include <vector>
#include <deque>
#include <string>
#include <boost/graph/adjacency_list.hpp>
#include <boost/graph/dijkstra_shortest_paths.hpp>
typedef boost::adjacency_list<boost::listS, boost::vecS, boost::directedS,
boost::no_property, boost::property<boost::edge_weight_t, int> > Graph;
typedef std::pair<int, int> Edge;
typedef boost::graph_traits<Graph>::vertex_descriptor Vertex;
enum { S, A, B, C, D, E, F, G, Z, N };
const std::string Names = "SABCDEFGZ";
// グラフを作る
Graph make_graph()
{
const std::vector<Edge> edges = {
{S, A},
{A, B},
{B, C},
{B, D},
{C, E},
{D, G},
{E, D},
{G, E},
{E, F},
{F, Z},
{G, Z},
};
// 辺の重みは1
const std::vector<int> weights(edges.size(), 1);
return Graph(edges.begin(), edges.end(), weights.begin(), N);
}
int main()
{
const Graph g = make_graph();
const Vertex from = S; // 開始地点
const Vertex to = Z; // 目的地
// 最短経路を計算
std::vector<Vertex> parents(boost::num_vertices(g));
boost::dijkstra_shortest_paths(g, from,
boost::predecessor_map(&parents[0]));
// 経路なし
if (parents[to] == to) {
std::cout << "no path" << std::endl;
return 1;
}
// 最短経路の頂点リストを作成
std::deque<Vertex> route;
for (Vertex v = to; v != from; v = parents[v]) {
route.push_front(v);
}
route.push_front(from);
// 最短経路を出力
for (const Vertex v : route) {
std::cout << Names[v] << std::endl;
}
}
出力:
S
A
B
D
G
Z
2つのグラフが同型か判定する
2つのグラフが同型かを判定するには、<boost/graph/isomorphism.hpp>で定義されるboost::isomorphism()関数を使用する。この関数は、引数として2つのグラフをとり、それらが同型であればtrue、そうでなければfalseを返す。 ここでは、以下の2つのグラフを比較する。
g1:

g2:

#include <iostream>
#include <vector>
#include <utility>
#include <boost/graph/isomorphism.hpp>
#include <boost/graph/adjacency_list.hpp>
typedef boost::adjacency_list<boost::listS, boost::vecS, boost::undirectedS> Graph;
const int vertex_count = 12;
Graph make_graph1()
{
const std::vector<std::pair<int, int>> edges = {
{ 0, 1}, { 1, 2},
{ 0, 2},
{ 3, 4}, { 4, 5},
{ 5, 6}, { 6, 3},
{ 7, 8}, { 8, 9},
{ 9, 10},
{10, 11}, {11, 7}
};
return Graph(edges.begin(), edges.end(), vertex_count);
}
Graph make_graph2()
{
const std::vector<std::pair<int, int>> edges = {
{ 9, 10}, {10, 11},
{11, 9},
{ 0, 1}, { 1, 3},
{ 3, 2}, { 2, 0},
{ 4, 5}, { 5, 7},
{ 7, 8},
{ 8, 6}, { 6, 4}
};
return Graph(edges.begin(), edges.end(), vertex_count);
}
int main()
{
const Graph g1 = make_graph1();
const Graph g2 = make_graph2();
const bool result = boost::isomorphism(g1, g2);
std::cout << "isomorphic? " << std::boolalpha << result << std::endl;
}
出力:
isomorphic? true
最小全域木を作る
グラフに含まれるすべての頂点を含む最小の部分グラフを、最小全域木(minimum spanning tree)と言う。
Boost.Graphには、最小全域木を作るためのアルゴリズムとして、以下の2つの関数が用意されている。
| 関数 | 説明 |
|---|---|
boost::kruskal_minimum_spanning_tree() | クラスカル法 |
boost::prim_minimum_spanning_tree() | プリム法 |
これらを以下のグラフに適用すると
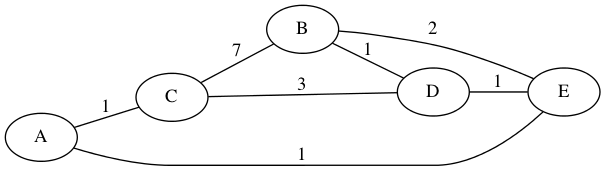
以下のような最小全域木(赤の太線部分)が手に入る。
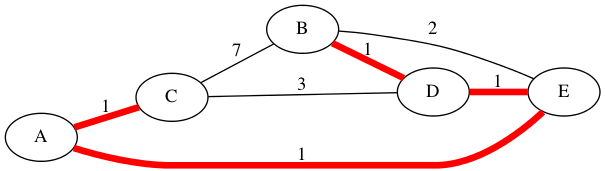
それぞれの使い方は以下のようになる。
クラスカル法
クラスカル法によって最小全域木を求めるboost::kruskal_minimum_spanning_tree()関数は、Output Iteratorで最小全域木の辺記述子(edge descriptor)を返す。
#include <iostream>
#include <boost/graph/adjacency_list.hpp>
#include <boost/graph/kruskal_min_spanning_tree.hpp>
typedef boost::adjacency_list<boost::listS, boost::vecS, boost::undirectedS,
boost::no_property, boost::property<boost::edge_weight_t, int> > Graph;
typedef std::pair<int, int> Edge;
typedef boost::graph_traits<Graph>::edge_descriptor EdgeDesc;
std::string Name = "ABCDE";
enum {A, B, C, D, E, N};
Graph make_graph()
{
const std::vector<Edge> edges = {
{A, C},
{B, D},
{B, E},
{C, B},
{C, D},
{D, E},
{E, A}
};
const std::vector<int> weights = {
1,
1,
2,
7,
3,
1,
1
};
return Graph(edges.begin(), edges.end(), weights.begin(), N);
}
int main()
{
const Graph g = make_graph();
std::vector<EdgeDesc> spanning_tree;
boost::kruskal_minimum_spanning_tree(g, std::back_inserter(spanning_tree));
for (const EdgeDesc& e : spanning_tree) {
std::cout << "(" << Name[boost::source(e, g)] << ","
<< Name[boost::target(e, g)] << ")" << std::endl;
}
}
出力:
(A,C)
(D,E)
(E,A)
(B,D)
プリム法
プリム法によって最小全域木を求めるboost::prim_minimum_spanning_tree()関数は、先行ノードマップ(predecessor map)として最小全域木を返す。
#include <iostream>
#include <boost/graph/adjacency_list.hpp>
#include <boost/graph/prim_minimum_spanning_tree.hpp>
typedef boost::adjacency_list<boost::listS, boost::vecS, boost::undirectedS,
boost::no_property, boost::property<boost::edge_weight_t, int> > Graph;
typedef std::pair<int, int> Edge;
typedef boost::graph_traits<Graph>::vertex_descriptor VertexDesc;
std::string Name = "ABCDE";
enum {A, B, C, D, E, N};
Graph make_graph()
{
const std::vector<Edge> edges = {
{A, C},
{B, D},
{B, E},
{C, B},
{C, D},
{D, E},
{E, A},
}
const std::vector<int> weights = {
1,
1,
2,
7,
3,
1,
1,
};
return Graph(edges.begin(), edges.end(), weights.begin(), N);
}
int main()
{
Graph g = make_graph();
std::vector<VertexDesc> parents(N);
boost::prim_minimum_spanning_tree(g, &parents[0]);
for (std::size_t i = 0; i < N; ++i) {
if (parents[i] != i) {
std::cout << "parent[" << Name[i] << "] = " << Name[parents[i]] << std::endl;
}
else {
std::cout << "parent[" << Name[i] << "] = no parent" << std::endl;
}
}
}
出力:
parent[A] = no parent
parent[B] = D
parent[C] = A
parent[D] = E
parent[E] = A
トポロジカルソート
無閉路有向グラフ(DAG : Directed Acyclic Graph)に順序を付けるトポロジカルソートは、<boost/graph/topological_sort.hpp>で定義されるboost::topological_sort()関数を使用する。
この関数は引数として、グラフ構造へのconst参照と、頂点リストを出力するOutput Iteratorをとる。(頂点リストは逆順で返されるため、boost::adaptors::reversedやrbegin()/rend()などで正順に直して使用する。)
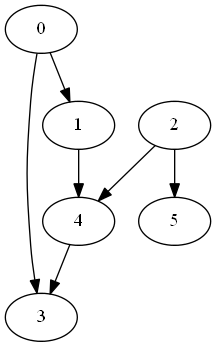
ここでは、以下のグラフにトポロジカルソートを適用する:
#include <iostream>
#include <vector>
#include <iterator>
#include <utility>
#include <boost/graph/adjacency_list.hpp>
#include <boost/graph/topological_sort.hpp>
#include <boost/range/algorithm/for_each.hpp>
#include <boost/range/adaptor/reversed.hpp>
typedef boost::adjacency_list<boost::listS, boost::vecS, boost::directedS> Graph;
typedef std::pair<int, int> Edge;
Graph make_graph()
{
const std::vector<Edge> edges = {
{0, 1}, {2, 4},
{2, 5},
{0, 3}, {1, 4},
{4, 3}
};
return Graph(edges.begin(), edges.end(), 6);
}
int main()
{
const Graph g = make_graph();
std::vector<int> result;
boost::topological_sort(g, std::back_inserter(result));
boost::for_each(result | boost::adaptors::reversed, [](int vertex) {
std::cout << vertex << std::endl;
});
}
出力:
2
5
0
1
4
3
出力から、有向グラフgがトポロジカルソートによって「2 → 5 → 0 → 1 → 4 → 3」の順序が付けられたことがわかる。
なお、boost::topological_sort()関数に、閉路のある有向グラフを指定した場合、boost::not_a_dag例外が投げられる。
一筆書きの経路を求める
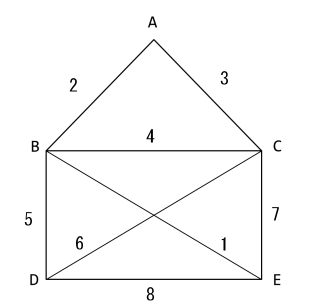
オイラー閉路というのを求めると、グラフの一筆書きの経路を得ることができる。ここでは、「サンタクロースの家」と呼ばれる無向グラフの一筆書きを求める。
Boost.Graphにはオイラー閉路のためのアルゴリズムは用意されていないが、以下のGitHubにあるshand::graph::euler_path()関数を利用することで、一筆書きを容易に求められる。
#include <iostream>
#include <deque>
#include <string>
#include <shand/graph/euler_path.hpp>
#include <boost/graph/adjacency_list.hpp>
enum {A, B, C, D, E, N};
const std::string name = "ABCDE";
int main()
{
typedef boost::adjacency_list<boost::listS, boost::vecS, boost::undirectedS> Graph;
typedef boost::graph_traits<Graph>::vertex_descriptor vertex_desc;
const std::vector<std::pair<int, int> > edges = {
{A, B},
{B, C},
{C, A},
{B, D},
{B, E},
{C, D},
{D, E},
{E, C}
};
const Graph g(edges.begin(), edges.end(), N);
std::deque<vertex_desc> path;
if (!shand::graph::euler_path(g, E, [&path](vertex_desc v) { path.push_front(v); })) {
std::cout << "euler path failed" << std::endl;
return 1;
}
BOOST_FOREACH (const vertex_desc& v, path) {
std::cout << name[v] << std::endl;
}
}
出力:
E
B
A
C
B
D
C
E
D
E, B, A, C, B, D, C, E, Dの順に頂点をたどれば一筆書きになることがわかった。
グラフをGraphviz形式(.dot)で出力する
グラフをGraphviz形式(.dot)で出力するには、<boost/graph/graphviz.hpp>をインクルードし、boost::write_graphviz()関数を使用する。この機能のために、別途ライブラリは必要としない。
write_graphviz()関数の引数:
| 引数 | 説明 |
|---|---|
| 第1引数 | 出力先のstd::ostream& |
| 第2引数 | グラフ構造へのconst& |
| 第3引数 | 出力方法のカスタマイズ方法 (ここでは、頂点名を出力するためにmake_label_writer()を使用している) |
#include <fstream>
#include <vector>
#include <string>
#include <boost/graph/adjacency_list.hpp>
#include <boost/graph/graphviz.hpp>
typedef boost::adjacency_list<boost::listS, boost::vecS, boost::directedS> Graph;
typedef std::pair<int, int> Edge;
enum { A, B, C, D, E, N };
const std::string name = "ABCDE";
int main()
{
const std::vector<Edge> edges = {
{A, B}, {A, C}, {A, D},
{B, E}, {C, E}, {D, E}
};
const Graph g(edges.begin(), edges.end(), N);
// graphvizの形式(*.dot)で出力
std::ofstream file("test.dot");
boost::write_graphviz(file, g, boost::make_label_writer(name.c_str()));
}
出力されたtest.dotファイル:
digraph G {
0[label="A"];
1[label="B"];
2[label="C"];
3[label="D"];
4[label="E"];
0->1 ;
0->2 ;
0->3 ;
1->4 ;
2->4 ;
3->4 ;
}
Graphvizのdotコマンドを使用してpngに変換:
dot -Tpng test.dot -o test.png
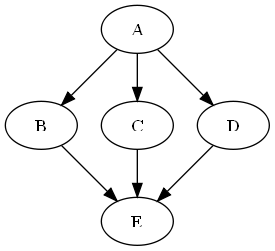
出力されたtest.png:
追加資料:
Graphviz形式(.dot)のデータを読み込む
Graphviz形式(.dot)のデータを読み込むには、<boost/graph/graphviz.hpp>で定義されるboost::read_graphviz()関数を使用する。この関数を使用するには、Boost Regex Libraryをリンクする必要がある。
ここでは、「グラフをGraphviz形式(.dot)で出力する」で出力したtest.dotファイルを読み込む。
read_graphviz()関数の引数:
| 引数 | 説明 |
|---|---|
| 第1引数 | 入力元のstd::istream& |
| 第2引数 | グラフ構造への参照 |
| 第3引数 | DOT言語のプロパティを処理するためのboost::dynamic_properties型変数への参照 |
#include <fstream>
#include <string>
#include <boost/graph/adjacency_list.hpp>
#include <boost/graph/graphviz.hpp>
#include <boost/graph/graph_utility.hpp>
typedef boost::adjacency_list<boost::listS, boost::vecS, boost::directedS> Graph;
enum { A, B, C, D, E, N };
const std::string name = "ABCDE";
int main()
{
std::ifstream file("test.dot");
Graph g;
boost::dynamic_properties dp(boost::ignore_other_properties);
boost::read_graphviz(file, g, dp);
boost::print_graph(g, name.c_str());
}
出力:
A --> B C D
B --> E
C --> E
D --> E
E -->
tested boost version is 1.51.0